Orca-Math Shows the Potential of Specialized Small Language Models

Microsoft Research has published a paper on Orca-Math, a specialized 7 billion parameter language model, that is showing impressive capabilities for its size. By outperforming much larger models in solving complex grade school math problems, Orca-Math showcases the potential of model specialization and iterative learning techniques.

Orca-Math which is fine-tuned from the Mistral 7B model, sheds light on the untapped potential of smaller language models when they are finely tuned for specialized tasks.

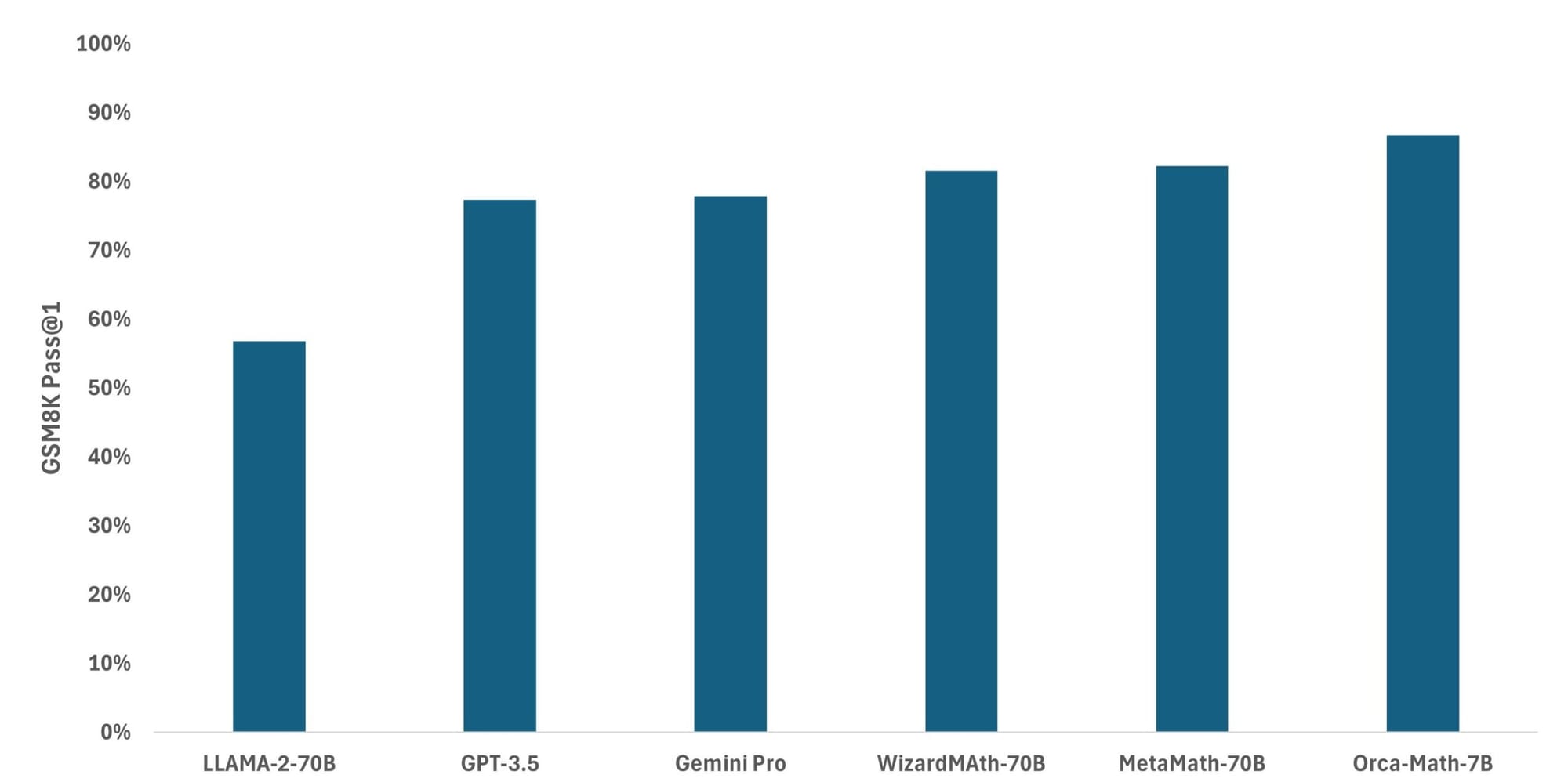
The model's performance on the GSM8K benchmark, a dataset of 8,500 high-quality grade school mathematical word problems, is particularly noteworthy. Orca-Math achieves an impressive 86.81% pass@1 accuracy, surpassing the performance of much larger general models like LLAMA-2-70, Gemini Pro, and GPT-3.5, as well as math-specific models such as MetaMath-70B and WizardMa8th-70B. This achievement is even more significant considering that the base model, Mistral-7B, only achieves 37.83% on the same benchmark.

The success of Orca-Math can be attributed to two key factors. First, the model was trained on a high-quality synthetic dataset of 200,000 math problems created using multi-agents (AutoGen). This dataset is smaller than other math datasets, which can contain millions of problems, resulting in faster and more cost-effective training. Second, in addition to traditional supervised fine-tuning, Orca-Math underwent an iterative learning process. This process allowed the model to practice solving problems and continually improve based on feedback from a teacher model.

The iterative learning process employed a teacher-student approach, where a large model (the teacher) created demonstrations for the smaller language model (the student) to learn from. The process involved three main stages: teaching by demonstration, practice and feedback, and iterative improvement. During the practice and feedback stage, the student model attempted to solve problems independently, generating multiple solutions for each problem. The teacher model then provided feedback on these solutions, guiding the student model towards the correct approach. If the student model was unable to solve the problem correctly after multiple attempts, the teacher model provided a solution. This feedback was then used to create preference data, showcasing both good and bad solutions to the same problem, which was used to retrain the student model. This process could be repeated multiple times, allowing for continuous improvement.

The implications of Orca-Math's success are significant. It demonstrates the value of smaller, specialized models in specific domains, where they can match or even surpass the performance of much larger models. This has the potential to make AI more accessible and cost-effective, as smaller models require less computational resources and can be trained on smaller datasets.

Furthermore, the iterative learning approach used in Orca-Math highlights the importance of continual learning and the role of feedback in improving language models. By allowing models to practice, receive feedback, and iteratively improve, we can develop AI systems that continuously adapt and refine their skills.

Microsoft has made the dataset used to train Orca-Math publicly available, along with a report detailing the training procedure. This transparency encourages further research and collaboration in the field, fostering the development of more efficient and effective language models.

As AI continues to advance, the lessons learned from Orca-Math will undoubtedly shape the future of language model development. By focusing on specialization, iterative learning, and the efficient use of resources, we can create AI systems that are not only powerful but also more accessible and adaptable to the needs of specific domains.